递归/回溯

递归是计算机科学中的一个重要概念。它是许多其他算法和数据结构的基础。然而，对于许多初学者来说，掌握它可能是一件非常棘手的事情。

每当递归函数调用自身时，它都会将给定的问题拆解为子问题。递归调用继续进行，直到到子问题成为一个不可以拆分的、可以直接求解的最简单问题。

为了确保递归函数不会导致无限循环，它需要包含：

一个简单的基本案例（basic case）（或一些案例），能够不使用递归来产生答案的终止方案。一组规则，也称作递推关系（recurrence relation），可将所有其他情况拆分到基本案例。注意，函数可能会有多个位置进行自我调用（这是分治算法）。

例题

21 合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
    if list1 == nil {
        return list2
    } else if list2 == nil {
        return list1
    } else if list1.Val < list2.Val {
        list1.Next = mergeTwoLists(list1.Next, list2)
        return list1
    } else {
        list2.Next = mergeTwoLists(list1, list2.Next)
        return list2
    }
}

💣 206 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func reverseList(head *ListNode) *ListNode {
    if head == nil || head.Next == nil {
        return head
    }
    newHead := reverseList(head.Next)
    head.Next.Next = head
    head.Next = nil
    return newHead
}

700 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

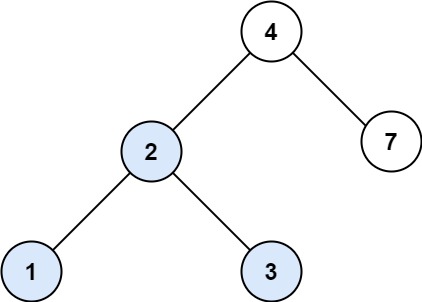
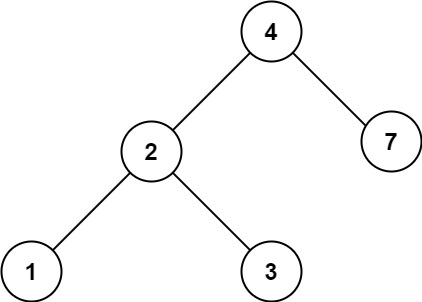
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 10⁷
root 是二叉搜索树
1 <= val <= 10⁷

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func searchBST(root *TreeNode, val int) *TreeNode {
    if root != nil {
        if val == root.Val {
            return root
        } else if val < root.Val {
            return searchBST(root.Left, val)
        } else {
            return searchBST(root.Right, val)
        }
    }
    return nil
}

70 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

func climbStairs(n int) int {
    hash := map[int]int{
        1 : 1,
        2 : 2,
        3 : 3,
    }
    return traverse(n, hash)
}

func traverse(n int, hash map[int]int) int {
    // 判断哈希表中是否有 n 记录
    if v, ok := hash[n]; ok {
        return v
    } else {
        // 判断哈希表中是否有 n - 2 记录
        if _, ok := hash[n - 2]; !ok {
            hash[n - 2] = traverse(n - 2, hash)
        }
        // 判断哈希表中是否有 n - 1 记录
        if _, ok := hash[n - 1]; !ok {
            hash[n - 1] = traverse(n - 1, hash)
        }
        // 存储 n 值记录
        hash[n] = hash[n - 1] + hash[n - 2]
        return hash[n]
    }   
}